传函设备的原理是什么?传函设备的原理构成
相信广大客户朋友在使用全欧光学传递函数测量仪的时候。对于原理性懵懵懂懂的概念,今天欧光科技针对相关内容做一些总结,以下就是作为总结性原理大纲,虽然很多时候没必要去深究其内在原理,但是了解相关原理后,能更好地服务我们的工作,大家一起来看看吧。
一、对比度
我们知道,一幅图像有亮暗程度之分,对比度就是用来描述光强最亮处与光强最暗处的比例关系:
M=(Imax-Imin)/(Imax+Imin)
这样我们就可以顺理成章的将物体理解为具有明暗特征的对象,从物理意义上即可以认为是各种频率的谱组成了一个物体,这样我们就可以通过傅里叶变换将物体的明暗分布展开为相应的级数或者积分,相信大家对傅里叶变换的朦胧的概念可能就停留在正余弦周期变换的函数,没错的,事实上,我们就可以简单的将光学系统对各种频率的正余弦信号的传递能力称之为光学传递函数,但请注意是光学传递函数。
二、空间不变线性系统
所谓线性系统是指能够满足“叠加原理”的系统,即对系统输入N个激励函数,则系统输出N个响应函数;如果把N个激励函数相叠加后输入到系统中,由系统输出的是与之相应的N个响应函数的叠加。满足线性条件的系统,其像平面上任一点处的光强度g(x,y)可以看作是物平面上每一点处的光强度f(x’,y’)在像平面(x,y)处所形成的光强的叠加。可用下式表示:
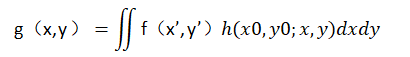
光学设备系统的空间不变性是指物面上不同的物点在像面上有相同形状的光能分布,用隐式函数表达如下:
h(x0,y0;x,y)=h(x-x0,y-y0)
虽然光学系统在不同视场会有不同的像差,但对经过像差校正的光学系统,像差随视场的变化是缓慢的,像面上总可以划出许多称为“等晕区”的小区域,在每个等晕区内光学系统为空间不变线性系统。
若物面分布函数为w(x0,y0),并假定物面上各亮点是非相干的,各个亮点经光学系统后的光强分布,即点扩散函数
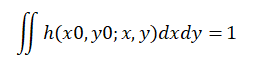
依据上述描述,像面上的光强分布可归结为下述隐式函数:
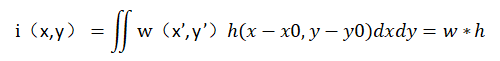
令i(x,y)、w(x,y)、h(x,y)经过傅里叶变换后分别为I(s,t)、W(s,t)、H(s,t),根据傅里叶变换理论中的定律可知:
I(s,t)=W(s,t)*H(s,t)*
上式表明,一个任意的非相干的光强分布w(x,y),可以看作是各种空间颜率的正余弦光强度分布的组合。每个正余弦分量W(s,t)称为物面分布函数w(x,y)中频率为(s,t)的谱。光学系统对w(x,y)成像的过程,就是将w(x,y)中的每一正余弦分量W(s,t)乘上一个相应的因子H(s,t), 构成像面分布函数i(x,y)的对应正余弦分量I(s,t),即像i(x,y)的谱。H(s,t)反映了光学系统对各种正余弦分量的传递特性。因此,光学系统的成像特性完全由H(s,t)反映出来,称为光学传递函数(Optical TransferFunction, OTF)。显然,它也可以用一个复函数形式来表示:
H(s,t)=T(s,t)*exp(-i*theta(s,t))
式中,T(s,t)表示调制传递函数,为光学传递函数的模,即我们熟知的MTF,theta(s,t)表示相位传递函数,为光学传递函数的辐角。
三、传函仪设备的构成
主体部分由一个离轴二反射结构组成一个大倍率的平行光管,将狭缝像扩展到无穷远的位置,用于待测光学系统来接收,并成像到设备的CCD中,CCD探测器采集到的带有原始数据和噪声的图像信号数字化然后进行去噪处理得到线扩散函数LSF,再对处理过的LSF进行傅里叶变换取模得到包括目标物在内的整个系统的MTF,最后对影响因素进行修正得到最终被测光电成像系统的MTF。
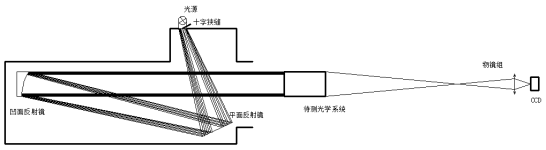
狭缝可看做矩形函数
f(x)=1/d*rect(x/d)
d为狭缝宽度,经过傅里叶变换后为sinc函数:
F(v)=sin(pi*d*v)/pi*d*v=sinc(d*v)*
设系统横向放大率为β,将系统MTF曲线统一到像面,则狭缝宽度对测量结果的影响为:
G(v)=sin(pi*β*d*v)/pi*β*d*v=sinc(β*d*v)
理论上讲狭缝的宽度越窄越好,但随着狭缝宽度变窄,透过它的能量减弱,信噪比降低,影响MTF测试精度,因此狭缝宽度不能太窄,即计算的系统MTF要除G(v)对狭缝宽度影响进行修正。由式G(v)可见,空间频率的第一个零点位置在1/β*d处,缝的宽度越大,零点位置则越向低频靠近。系统的极限分辨率Rmax。由于结果修正要除以G(v),所以只有当Rmax在零点的左侧,修正才有意义。即需要满足:*
Rmax<1/β*d*
即:d<1/β*Rmax=(f仪/f待测)/Rmax,狭缝法测试时狭缝宽度选取要满足此条件。
四、采样定理
采样定理,又称香农采样定理,奈奎斯特采样定理,是信息论,特别是通讯与信号处理学科中的一个重要基本结论。在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>=2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;对应到光敏传感器上,即对应光信号应至少在两个像元内,才能保证图像不失真的进行输出,假设对应3.45um像元,计算其奈奎斯特频率为:
R_N=1/2*pixel=1/(3.45*2)=145lp/mm*
衍射极限频率根据瑞利判据,即当两个斑点刚好能分辨的极限,计算公式为:
R_diff=1/(1.22*中心波长*F#)*
截止频率,即纵坐标值为零对应的空间频率,计算公式为:
R_cutoff=1/pixel_
大家应注意区分这三种频率,定义是不一样的。
-

半导体光刻物镜的精度对于芯片制造有哪些具体影响?
在当今科技高速发展的时代,芯片宛如现代社会的“工业粮食”,广泛应用于从智能手机、电脑到汽车、工业控制等诸多领域,深刻改变着人们的生活与生产方式。而在芯片制造这一复杂且精密的工艺链条中,半导体光刻物镜的精度扮演着举足轻重、堪称“命门”的关键角色,诸多环节与之紧密相连,牵一发而动全身。
2024-11-25
-

什么是微波光子学?微波光子学的应用和特点
在信息技术迅猛发展的今天,微波光子学作为一门融合微波工程和光子学的新兴交叉学科,正逐渐在通信技术领域崭露头角。它利用光子技术处理微波频率范围内的信号,为高频信号的生成、传输、处理和分析提供了创新的解决方案。本文将探讨微波光子学的关键应用、技术特点,并探讨它是否预示着通信技术的未来。
2024-11-25
-
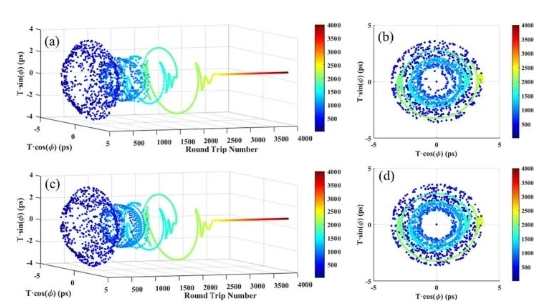
光学前沿的新进展:矢量纯四次孤子分子光纤激光器研究新进展
在光学领域,孤子(soliton)是一种特殊的光脉冲,它在非线性介质中传播时能够保持其形状不变。近年来,随着非线性光学和光纤激光器技术的发展,孤子的研究已经从传统的二次孤子扩展到了更高阶的孤子,如纯四次孤子。本文将概述矢量纯四次孤子分子光纤激光器的最新研究进展,这一领域的发展为光学通信、光逻辑系统和高分辨率光学等领域带来了新的机遇。
2024-11-25
-

【光学前沿】阿尔托大学开创光涡旋新设计,推动光数据传输革命
在数据存储和传输需求日益增长的今天,寻找更高效的方法来编码和传输大量数据变得至关重要。阿尔托大学的最新研究成果为我们提供了一种创新的解决方案:通过在光纤中使用准晶体传输数据的光涡旋。这项突破性的设计方法不仅理论上可以创建任何类型的光涡旋,而且在实际应用中展示了极高的拓扑电荷,为光数据传输开辟了新的可能性
2024-11-22







