光学前沿的新进展:矢量纯四次孤子分子光纤激光器研究新进展
在光学领域,孤子(soliton)是一种特殊的光脉冲,它在非线性介质中传播时能够保持其形状不变。近年来,随着非线性光学和光纤激光器技术的发展,孤子的研究已经从传统的二次孤子扩展到了更高阶的孤子,如纯四次孤子。本文将概述矢量纯四次孤子分子光纤激光器的最新研究进展,这一领域的发展为光学通信、光逻辑系统和高分辨率光学等领域带来了新的机遇。
一、纯四次孤子的特性与应用前景
纯四次孤子与传统孤子不同,它们由四阶色散和非线性平衡产生,并表现出独特的特性。这些孤子具有长振荡尾,使得孤子捕获在分子内子脉冲之间或沿着双折射光纤的两个偏振轴之间变得容易。这种特性为研究孤子分子的相互作用和运动动力学提供了新的机会,有助于揭示孤子分子复杂性的新机制。
二、矢量纯四次孤子分子的理论研究
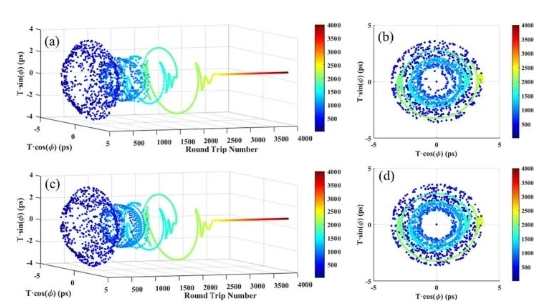
Zhu等人通过求解由四阶色散引起的耦合金兹堡-朗道方程,理论探索了矢量纯四次孤子分子的瞬态动力学。研究发现,矢量纯四次孤子分子展现出多种实时动力学行为,包括稳态和脉动,这些行为源于分子内部和正交轴之间的多尺度能量交换,且受到非线性效应的影响。
三、实验观察与动力学分析
实验中,研究人员观察到矢量纯四次孤子分子的构建过程,包括分裂、脉动和同步。他们还绘制了构成分子相关内部自由度的脉冲分离和相位差的相关动力学。这些研究结果不仅为纯四次孤子带来了新的见解,而且为双折射光纤的高能光纤激光器提供了全新的潜在应用前景。
四、数值仿真与模型建立
为了更好地理解矢量纯四次孤子分子的行为,研究人员建立了一个数值仿真模型,该模型由掺铒光纤(EDF)、可饱和吸收体(SA)和无源单模光纤(SMF)组成。通过耦合Ginzburg-Landau方程计算腔内脉冲的传播,研究人员能够模拟并分析孤子分子的演化动力学。
矢量纯四次孤子分子的研究不仅丰富了我们对耗散非线性系统中高阶色散引起的动力学的理解,而且为孤子的形成提供了新的见解。这些发现对于光纤激光器的设计和应用具有重要意义,尤其是在高能光纤激光设备领域。随着研究的深入,我们可以期待在未来的光学技术中看到更多基于纯四次孤子的创新应用。
-

半导体光刻物镜的精度对于芯片制造有哪些具体影响?
在当今科技高速发展的时代,芯片宛如现代社会的“工业粮食”,广泛应用于从智能手机、电脑到汽车、工业控制等诸多领域,深刻改变着人们的生活与生产方式。而在芯片制造这一复杂且精密的工艺链条中,半导体光刻物镜的精度扮演着举足轻重、堪称“命门”的关键角色,诸多环节与之紧密相连,牵一发而动全身。
2024-11-25
-

什么是微波光子学?微波光子学的应用和特点
在信息技术迅猛发展的今天,微波光子学作为一门融合微波工程和光子学的新兴交叉学科,正逐渐在通信技术领域崭露头角。它利用光子技术处理微波频率范围内的信号,为高频信号的生成、传输、处理和分析提供了创新的解决方案。本文将探讨微波光子学的关键应用、技术特点,并探讨它是否预示着通信技术的未来。
2024-11-25
-

光学前沿的新进展:矢量纯四次孤子分子光纤激光器研究新进展
在光学领域,孤子(soliton)是一种特殊的光脉冲,它在非线性介质中传播时能够保持其形状不变。近年来,随着非线性光学和光纤激光器技术的发展,孤子的研究已经从传统的二次孤子扩展到了更高阶的孤子,如纯四次孤子。本文将概述矢量纯四次孤子分子光纤激光器的最新研究进展,这一领域的发展为光学通信、光逻辑系统和高分辨率光学等领域带来了新的机遇。
2024-11-25
-

【光学前沿】阿尔托大学开创光涡旋新设计,推动光数据传输革命
在数据存储和传输需求日益增长的今天,寻找更高效的方法来编码和传输大量数据变得至关重要。阿尔托大学的最新研究成果为我们提供了一种创新的解决方案:通过在光纤中使用准晶体传输数据的光涡旋。这项突破性的设计方法不仅理论上可以创建任何类型的光涡旋,而且在实际应用中展示了极高的拓扑电荷,为光数据传输开辟了新的可能性
2024-11-22







